Smoky Cogs

Statistics is not exactly the easiest of fields to work with. I am not talking about the “how many hits has my blog had today” type of stats, but rather, the “what is the standard deviation of today’s hits compared to the rest of the month” type of stats.

I studied a course in statistics at university many years ago, and I still shudder at some of the mathematical techniques used.

Well, as a programmer, these days, I would just use a statistics library to do the heavy lifting for me, sparing my brainpower for coding instead.

One such library I have found for JavaScript, jStat, makes inserting statistical data and graphs ridiculously easy, and there are several samples on their website detailing how to use the library.

Being a JavaScript library, this can add a lot to just about any web application.

I can think of many, many uses for this…

People tend to think of abacuses (or is it abaci) as archaic devices with no relevance today, except as an aid to teach children basic arithmetic. For the most part, they would be right.

There is, however, a lot of value the abacus can give even in this modern computer age. Not only can experienced abacus users do amazingly quick calculations with them, but the methods used to calculate can be useful for computers too.

One example is with calculating a square root, which Martin Guy discusses in a paper he wrote in 1985.

He details how the algorithm he found in the book, The Fundamental Operations in Bead Arithmetic: How to Use the Chinese Abacus by C.C. Woo, to calculate the square root using an abacus, when implemented as a computer routine, is actually several times faster than many standard computer implementations of the square root function at that time.

I think it would be interesting to see if now, 25 years later, this routine would still be faster than standard square root functions.

It is incredible that a centuries old computing device can still have an impact even today.

If you are a programmer, then it is highly likely that you are aware of Stack Overflow. You might even be aware that Stack Overflow has a bunch of sister sites, which can be found at Stack Exchange.

One of these, math.stackexchange.com which I found particularly interesting has just gone out of beta.

Like Stack Overflow, this site is a Q and A site, but instead of focusing on programming, it focuses on mathematical questions.

No doubt that this site will be a lot of help to programmers as well as mathematicians.

A few days ago I posted blog containing a wealth of mathematical theory. Today I found another great mathematical resource.

This site by Paul Bourke is particularly interesting to programmers who want to develop graphical rich applications such as games, since it has a huge amount of articles explaining how 2D and 3D geometry,which forms the heart of graphics programming.

MathWorld, which is run by Wolfram, is a very impressive collection of mathematical resources that would make any maths geek quiver with excitement.

It is not for the fainthearted, though. Don’t expect simple articles on basic high school maths. While there are more basic topics, much of the mathematics listed on the site involve some rather hectic mathematical theory.

The site does classify the topics well, and if you really do need to know what the square root of 2 is, or what an Eisenstein Series, then enjoy.

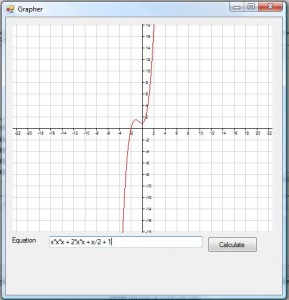
Creating an application to draw graphs of mathematical equations has two components to it, namely, parsing the equation and drawing the results.

Parsing an equation is quite a complicated endeavor. However, I found on the internet a very useful C# library that parses equations very well called dotMath by Steve Hebert. You can visit the website for the library at . Rather than write my own library, I used this library to do all the parsing for me.

The fun part – for me anyway – is trying to draw the graph of an expression. I created a Windows Forms control that contains a picture box that fills the entire control. This picture box will contain the graph that we draw.

The actual generation of the image we are going to draw happens using a Bitmap object.

We set up the pens and brushes we need for the axis, graph, grid and background using the configuration settings that the class contains.

If the flag to draw the axes is set, we first draw the x and y axes, and then label it, using the scale we specify. The offset allows us to move the graph so that the centre of the screen does not need to be the position (0,0), which is the default. The LabelIncrement determines how many pixels apart the labels need to be.

If we set the draw grid flag to true, we also draw a grid, which will make it easier to see what value the graph shows.

Drawing the axes and grid works by taking the centre point and working out along each axis to the end of the screen.

Now that we have set everything up, we can draw the graph.

Here is where we use the dotMath class to parse our equation we want to draw.

So given an example equation of something like “x*x + 3 * X + 23″ or “sin(x)”, we iterate through each pixel, and get the value of x at that pixel based on the scale and offset.

We then replace the character “x” in the equation with our value for x, and pass the string to the equation parser, which then calculates the y value.

From this we can, again using the scale and offset, determine the y value of the coordinate we need.

To actually draw the point, we draw a line from the previous pixel to the current pixel which we have calculated.
continue reading…

The greatest common divisor of two numbers is the largest number that divides evenly into both numbers.

The method of calculating this is is to use a little bit of recursion.

If the numbers are even, then work out the GCD by dividing both numbers by 2 and passing as parameters to the GCD function recursively, multiplying the result by 2.

If only one number is even, then pass that number divided by 2, and the whole second number to the GCD function to get the GCD.

If both numbers are odd, then call the GCS function with the average of the two numbers and the second number as the parameters.

If the numbers are equal then return that number, and if either number is equal to then return 1.

By the time execution reached the top again after the recursion, you should have the greatest common divisor as your resulting number.

        public static int GCD(int A, int B)
        {
            if (A == B)
            {
                return A;
            }
            if ((A == 1) || (B == 1))
            {
                return 1;
            }
            if ((A % 2 == 0) && (B % 2 == 0))
            {
                return 2 * GCD(A / 2, B / 2);
            }
            else if ((A % 2 == 0) && (B % 2 != 0))
            {
                return GCD(A / 2, B);
            }
            else if ((A % 2 != 0) && (B % 2 == 0))
            {
                return GCD(A, B / 2);
            }
            else
            {
                return GCD(Math.Abs(A - B) / 2, B);
            }

        }