This is the first in a series of posts that I am going to do on generating fractals using C#. All code was compiled using Visual Studio 2008.
The source code for the application, which includes all the fractals which will be covered in the series is available for download here.
Everybody always covers the Mandelbrot as the fractal of choice, so, in doing things a little differently, I decided to start with plasma fractals, and leave the Mandelbrot until later.

A plasma fractal

Assigning values to the four corners
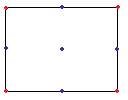
Find average for edges and centre
The next step is to find the midpoint of each side, and at that point, calculate the average value of the two points that this point is bisecting. A midpoint is also calculated, which is in the centre of the rectangle, which is the average of all four corners plus a random displacement.
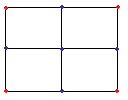
Repeat process with the four new rectangles
After the values have been calculated, the values can be converted to colours using any method you like. Using the raw values unaltered will create a greyscale image very well with only adjusting the value to put it in the correct range.
Now, in the code to do this (which can be found in Plasma.cs in the source download), first, we have a few global variables
public double gRoughness;
public double gBigSize;
FastRandom rnd;
The roughness is amount in which we are going to vary the value by for the midpoint.gBigSize is defined as the width plus the height of the image we are generating. FastRandom is a random number generator, which works exactly like the builtin random number generator, except that it is faster.
Our starting point is the Generate function that return a two-dimensional array of values where each entry in the array corresponds to an xy coordinate and the value is the calculated value, which will be converted into a colour.
public double[,] Generate(int iWidth, int iHeight, double iRoughness)
{
double c1, c2, c3, c4;
double[,] points = new double[iWidth+1, iHeight+1];
//Assign the four corners of the intial grid random color values
//These will end up being the colors of the four corners
c1 = rnd.NextDouble();
c2 = rnd.NextDouble();
c3 = rnd.NextDouble();
c4 = rnd.NextDouble();
gRoughness = iRoughness;
gBigSize = iWidth + iHeight;
DivideGrid(ref points, 0, 0, iWidth, iHeight, c1, c2, c3, c4);
return points;
}
This function sets the four initial corners, and sets the global variables, and then starts the recursion to generate the rest of the points by calling DivideGrid, which is what follows next. The most import point here is that the array containing the points is passed as a reference variable to DivideGrid, so that as it recurses, it can update the points accordingly.
public void DivideGrid(ref double[,] points, double x, double y, double width, double height, double c1, double c2, double c3, double c4)
{
double Edge1, Edge2, Edge3, Edge4, Middle;
double newWidth = Math.Floor(width / 2);
double newHeight = Math.Floor(height / 2);
if (width > 1 || height > 1)
{
Middle = ((c1 + c2 + c3 + c4) / 4)+Displace(newWidth + newHeight); //Randomly displace the midpoint!
Edge1 = ((c1 + c2) / 2); //Calculate the edges by averaging the two corners of each edge.
Edge2 = ((c2 + c3) / 2);
Edge3 = ((c3 + c4) / 2);
Edge4 = ((c4 + c1) / 2);//
//Make sure that the midpoint doesn't accidentally "randomly displaced" past the boundaries!
Middle= Rectify(Middle);
Edge1 = Rectify(Edge1);
Edge2 = Rectify(Edge2);
Edge3 = Rectify(Edge3);
Edge4 = Rectify(Edge4);
//Do the operation over again for each of the four new grids.
DivideGrid(ref points, x, y, newWidth, newHeight, c1, Edge1, Middle, Edge4);
DivideGrid(ref points, x + newWidth, y, width - newWidth, newHeight, Edge1, c2, Edge2, Middle);
DivideGrid(ref points, x + newWidth, y + newHeight, width - newWidth, height - newHeight, Middle, Edge2, c3, Edge3);
DivideGrid(ref points, x, y + newHeight, newWidth, height - newHeight, Edge4, Middle, Edge3, c4);
}
else //This is the "base case," where each grid piece is less than the size of a pixel.
{
//The four corners of the grid piece will be averaged and drawn as a single pixel.
double c = (c1 + c2 + c3 + c4) / 4;
points[(int)(x), (int)(y)] = c;
if (width == 2)
{
points[(int)(x+1), (int)(y)] = c;
}
if (height == 2)
{
points[(int)(x), (int)(y+1)] = c;
}
if ((width == 2) && (height == 2))
{
points[(int)(x + 1), (int)(y+1)] = c;
}
}
}
If the rectangle is bigger than a pixel, then this function now calculates the average for the four edges, as well as the average of all four corners with the displacement added for the centre.
After this the values are rectified, so that the values stay within the bounds set, and the DivideGrid function is called again for each new rectangle.
If the rectangle is a pixel big, then we have reached the base case, and only the centre is calculated and assigned. At this point the function does not recurse any deeper but now returns.
Lastly we just have Rectify and Displace which we have dealt with already. Displace just calcualtes a random displacement based on the size of the rectangle and the roughness.
private double Rectify(double iNum)
{
if (iNum < 0)
{
iNum = 0;
}
else if (iNum > 1.0)
{
iNum = 1.0;
}
return iNum;
}
private double Displace(double SmallSize)
{
double Max = SmallSize/ gBigSize * gRoughness;
return (rnd.NextDouble() - 0.5) * Max;
}
Stay tuned for future posts in this series on fractals….
Comments